Q4:
Laws of Logarithms
Share
Previous
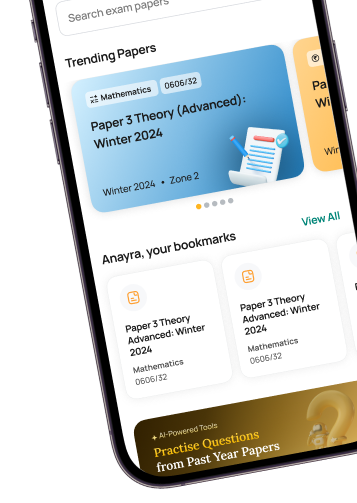
Questions:
4/1
Topic: Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Solution
PRACTISE
Similar Questions
LEARN
Concepts with Sparky
More Questions from this Topic
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Determine the value of each of the following.a. $\log_{5} 5$b. $\log_{5} 25 + \log_{5} 2$c. $\log_{5} 100 - \log_{5} 4$
Winter
3
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Let $a = \ln 4$ and $b = \ln 8$. Write down the following expressions in terms of $a$ and $b$:a. $\ln 16$b. $\ln 2$c. $\ln 64$
Winter
2
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Rewrite the expression $4\ln 3 - \ln 9$ in the form $\ln k$, where $k \in \mathbb{Z}$.
Winter
1
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Solve $3\ln 4 - \ln 16 = -\ln y$ for $y$.
Winter
3
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
(a) Calculate the value of: (i) $\log_3 27$ (ii) $\log_4 \left( \frac{1}{16} \right)$ (iii) $\log_{10} 1000$(b) Hence, solve $\log_3 27 + \log_4 \left...
Winter
3
More Questions from year 2023
Theory
Reciprocals
A sequence starts with 4 and increases in such a way that the second term is 8 and the third term is 12.(a) Determine the constant increment, $c$, for...
Winter
2
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Determine the value of each of the following.a. $\log_{5} 5$b. $\log_{5} 25 + \log_{5} 2$c. $\log_{5} 100 - \log_{5} 4$
Winter
3
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Let $a = \ln 4$ and $b = \ln 8$. Write down the following expressions in terms of $a$ and $b$:a. $\ln 16$b. $\ln 2$c. $\ln 64$
Winter
2
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Rewrite the expression $4\ln 3 - \ln 9$ in the form $\ln k$, where $k \in \mathbb{Z}$.
Winter
1
Theory
Laws of Logarithms (Sum, Difference, Exponent and Change of Base Law)
Solve $3\ln 4 - \ln 16 = -\ln y$ for $y$.
Winter
3
Theory
Logarithms
(a) Calculate the value of: (i) $\log_3 27$ (ii) $\log_4 \left( \frac{1}{16} \right)$ (iii) $\log_{10} 1000$(b) Hence, solve $\log_3 27 + \log_4 \left...
Winter
3